Offensive Balance

Inspired by a tweet from Chris Brown a.k.a smartfootball on this interesting but largely meaningless article from Rivals I decided to put together a post on offensive balance.  This is going in place of my normal Monday post and I should be back in a week or so with Brian’s requested special teams primer.

Game Theory and Play Calling

Game theory suggests that teams will adjust their choices so that the average value of each choice (run or pass) will be equal. We also know that not all coaches are rational decision makers and there are likely very few who understand what game theory is.  That is where nerds like myself come it to explain on blogs and help them understand.

The thinking goes like this: a team is really good at running the ball and really bad at passing the ball, but they are perfectly “balanced,” half their plays are rushes and half are passes.  Since there is more value on a running play than a passing play, it doesn’t make sense to be calling so many pass plays, so the first adjustment happens and this team starts calling more rushes to take advantage of their more efficient running game.  At some point, the defense responds to the new strategy and begins to stack against the run which of course makes success in the passing game easier. If the offense is playing optimal strategy, their final mix will be one that garners the same value for each play, regardless of whether it is a run or a pass, even if the distribution of plays is not 50/50.

Charts? Charts!

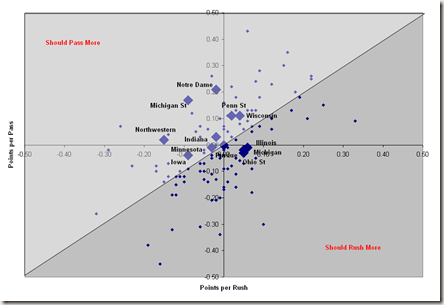
This is how every team in the country fared on a per down basis in both rush and pass. The diagonal line represents balanced results on a per play basis.  Teams on the top right are balanced and successful, teams on the bottom left are balanced and unsuccessful.  Teams to the left of the line (Northwestern, Iowa, Michigan St, Notre Dame, Penn St, Wisconsin, Indiana and Minnesota) should pass the ball more to become more optimal where teams below the line (Michigan, Ohio St and Illinois) have the opportunity to run the ball more to become more optimal.  Purdue sits right at the intersection of all lines, balanced and mediocre.  Most of the teams in the Big 10 where within reach of balance with the notable exceptions of Michigan St and Notre Dame, two teams that couldn’t get their rushing outputs to match their passing success. Time for another chart.

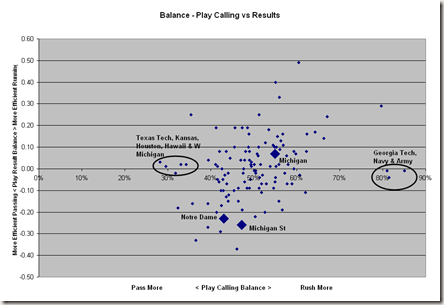
In this chart you can see how balance in calls does not necessarily equal balance in output.  In fact, some of the least balanced play callers, on both ends of the spectrum no less, produced the most balanced results in output.  Teams who rushed over 80% of the time like Georgia Tech, Navy and Army got almost the same value from passes as they did form rushes.  On the other end, pass happy squads like Texas Tech, Kansas and Houston saw similar production on a per play basis from their running games as they did from their passing games.  These teams are still running or passing teams, but their play calling balance has found an equilibrium where they are maximizing their total points by finding balance, even if they are calling a lot more of one type of play than another.

You can see that Michigan St and Notre Dame are both outliers in their respective deviations in success between run and pass, despite being towards the middle (especially MSU) when it comes to run pass selection.

Other Notes

This data does not include games for any team versus non D1 opponents (Baby Seal U).  Only plays when the lead is 2 TDs or less or if the game is still in the first half are counted.  Points per play uses my expected points model and is adjusted based on opponents played. Interceptions are included in this analysis but fumbles, fumble returns and interception returns are not.  Including fumbles pushes the balance to passing as fumbles are more likely to occur on running plays than pass plays.  Most of that difference is negated if you include returns as interceptions are much more likely to be returned than fumbles and the total value of interception returns is nearly equal to the difference between fumbles on running plays versus passing plays.  The net of it all is that excluding fumbles and returns does not materially affect any of the data above. 

Explanation of system

The basics:
+ is good, - is bad. Everything associated with a rating is given a +/- and a number. The number corresponds directly to a scoreboard equivalent. A player or team with a rating of +7 means that that they are one full touchdown better than average over the course of a game. Likewise, a rating of -7 means that they are a full touchdown per game worse than average.

How do I arrive there?
I havea database of play by play for all the games for a given group (NCAA or NFL) for the whole season. Based on all of this data, each combination of down, distance and line of scrimmage is assigned a point value. A 1st and 10 at your own 20 will, on average yield 1.52 points, or a little more than 1 touchdown every 5 possessions. Each play is then evaluated based on how many points were expected before the play and then after. Examples:

Oklahoma has a 3rd and 1 at their own 36. Expected points: 1.81
Chris Brown rushed for a 6 yard gain and a new 1st down. Expected points: 2.44
Chris Brown is awarded +.63 for getting the 1st down and moving Oklahoma closer to a TD.

Oklahoma has a 2nd and 10 at their own 24. Expected points: 1.44
Sam Bradford passes complete to Manuel Johnson for 6 yards. Expected points: 1.56
Bradford and Johnson both receive +.12 for the 6 yard gain. The gain was the same as before, but 6 yards on 3rd and 1 are a lot more valuable than on 2nd and 10, thus the points awarded are greater.

All of these individual plays are then added up and all of the individual players and teams are awarded a cumulative score. That cumulative score is then adjusted based on the strength of the opponents unit. Colt McCoy's performance against Oklahoma began as a +9 but because he did it against the Oklahoma defense, the value was adjusted to +24. Conversely, in the controversial Washington/BYU game in week 2, BYU QB Max Hall began with a +16 but because the Washington pass defense is so weak, his score was demoted to a +6. The adjustments can be much greater for college football vs the NFL as the level of competition is much more varied at the collegiate level.

How do you account for turnovers?
There are 2 components to every turnover. The loss of opportunity for the offense and the resulting gain of opportunity for the defense. For the first half, the player who commits a turnover is deducted the same amount as if he would have failed to gain a first down on the play. However a second component is then added. Depending on where the opponent takes over, a further deduction is given. An interception 35 yards down field is essentially the same as a punt, so no additional penalty is given. However, if that interception is returned for 50 yards, the opponent has not only recovered the punting distance, but 15 additional yards as well. To calculate the change, I assume that if the drive had ended at that point, it would have given the opponent 35 yards from the line of scrimmage, but no closer than the 20 yard line. The difference in value between this spot and the value of the spot where the return ended (or 7 pts if it was returned for a TD) is deducted from the offensive play value.

How do you account for competition?
After all the game are entered, each unit gets all of their pts added up and then divided by the number of plays. A perfectly average unit will come out to 0.00 a good unit may be +0.30. Then every play's value is re-entered to account for the level of competition. A run worth +1.00 against a bad rush defense could only be worth +0.70 for the offense. However, if the rush offense is also very bad, the defense may be docked -1.30 for the play. A play will not have the same value for the offense and defense because their ratings are not the same. In fact, both teams can end the game with a positive score if both are good and the game is tight, or both teams could end with a negative score if both are bad and neither shines.